里约热内卢Yokota，英国布里斯托尔大学
洛伦娜·a·芭芭，波士顿大学
Matthew Knepley，芝加哥大学
在计算科学中的许多应用都需要基于实时数据来近似一个函数。当数据在一定意义上在其域内“分散”时，一种非常强大的技术是径向基函数（RBF）插值。多年来，RBF插值的广泛应用受到其数值难度和费用的限制。事实上，在它们的数学表达式中，RBF方法产生了一个病态线性系统，对于超过几千个数据点的直接解变得令人望而却步。
我们已经开发了一种用于RBF插值的并行算法，该算法具有O(N)复杂度，需要O(N)存储，并且可以出色地扩展到1,000个进程。该算法采用基于受限加性Schwarz法（RASM）的GMRES迭代解算器作为前置条件，采用快速矩阵向量算法。以前的快速RBF方法是使用多重二次和多谐基函数开发的，其复杂度最多为O（N log N）。相比之下，本方法使用方差较小的高斯分布。高斯基函数的快速衰减使得迭代求解器即使在子域很小的情况下也能快速收敛。该方法是使用PETSc库（开发者版本）并行实现的。数值实验证明了其在Blue Gene/L （700 MHz PowerPC处理器）的1024个处理器上处理超过5000万个数据点的RBF插值问题的能力，时间为106秒（19次迭代，误差容限为10e - 15）。
并行代码在开源模型中是免费提供的。http://code.google.com/p/petrbf/
径向基函数（RBF）插值
近似一个函数：
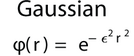
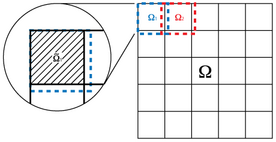
领域分解方法
领域分解方法可以通过分布问题来求解高度并行结构上的线性系统。
数学上可以写成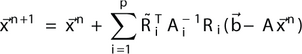
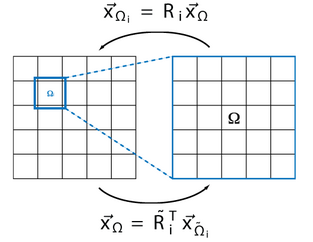
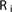是限制运算符，它将元素映射到重叠的子域。
是投影算子，它将元素映射到重叠的子域。
受限加性Schwarz法（RASM）
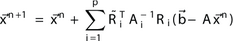
对于高斯基函数，RASM作为一种预处理和并行化技术。这个特殊的基函数是RASM的完美匹配。
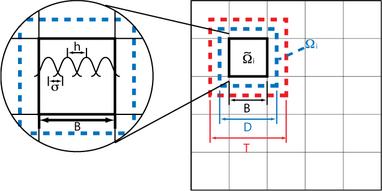
RASM中的参数
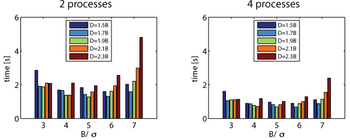
非重叠子域B、重叠子域D和矩阵向量乘法T中要考虑的域的大小对计算时间影响较大。与s相比，这些域的相对大小产生了差异。这与元素的数量和进程的数量无关。
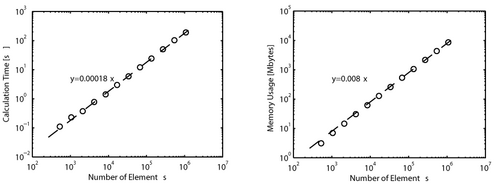
复杂性和内存使用
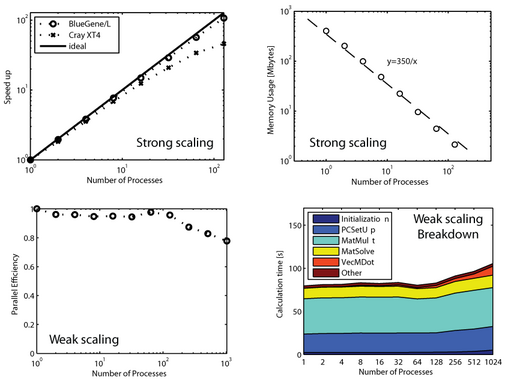
当元素个数N增加时，本方法的计算时间和内存使用量随O(N)的增加而增加。这优于其他缩放为O（N log N）的RBF插值方法。
并行可扩展性
对于并行计算，我们使用了波士顿大学的Blue Gene/L机器。
